Designing Sequential Circuits through Verilog

Designing Sequential Circuits through Verilog

Designing Sequential Circuits through Verilog: Combinational logic is the digital system where the output levels at any instant of time depend only upon the levels present at the inputs at that time. However, there are many applications in which digital outputs need to generate a sequence in which the input signals receive, which combinational circuits cannot accomplish. In sequential logic, the outputs are not only dependent on the level present at the inputs at that time, but also on the current state of the circuit. Feedback from the output back to the data provides history. Thus, combinational circuits and memory elements make sequential circuits.

Sequential Versus Combinational

The primary difference is the output variables at any instant of time depend only on the present input variables in combinational circuits. In contrast, the sequential course the output variables at any moment depends not only on the current input variables but also on the history of the system.

Former circuits do not require any memory but later needs to store the past of the input variables. Hence, the circuit requires a memory unit. Sequential circuits are slower in comparison to combinational circuits and are comparatively harder to design.

The sequential circuits are classified as synchronous sequential circuits and asynchronous sequential circuits depending on the timing of their signals. So lets see more Designing Sequential Circuits through Verilog

Synchronous Sequential Circuit

The change in input signals can affect memory elements upon the activation of clock signals. The clock is a systematically happening pulsation. A pulse generator generates it. So, the maximum operating speed of the clock depends on time delays involved. “Edge triggered clocked flip-flops.” are the memory elements.

Asynchronous Sequential Circuit

The change in input signals can affect memory element at any instant of time. Because of the absence of a clock, this circuit can operate faster than the synchronous circuit. In this circuit, either “unclocked flip-flops” or time delay elements act as memory elements. They work as “level-triggered course” also, which makes them hard to model.

Latches and Flip-flops

A primary memory cell is a circuit that stores one bit of information. Additionally, this one-bit memory element is called a flip-flop. The flip-flop is made up of an assembly of logic gates. Even though a logic gate by itself has no storage capacity, but several logic gates connect in ways that permit information storage. Flip-flops are the essential unit of the most sequential circuit. A flip-flop, known more formally as a bistable multi-vibrator, has two stable states. It can remain in either of the states indefinitely, and the state can be changed by applying the proper triggering signal. A flip flop is a synonym to binary or one-bit memory. We can also realize the flip-flop by the cross-connection of NAND gates or NOR gates in the feedback loop.

In its purest form, a flip-flop is called a ‘Latch,’ since it latches (or locks) data in it. In latch, there is no facility to read its contents. They are temporary storage devices. Ideally, it accommodates for storing information between processing units and input units.

Difference

The main difference between a latch and a flip-flop is in the method to trigger the state. Latches are generally unclocked or level-triggered whereas flip flops are edge-triggered. Triggering initiates the operation of latches or flip-flops. Its primary purpose is to synchronize latches or flip-flops.

It is classified into Level triggering and Edge triggering. In level triggering, input signals affect the flip-flop only when the clock is at logic ‘1’ in case of positive level triggering and logic ‘0’ in case of negative level triggering.

In edge triggering, input signals affect the flip-flop only if they are present at the positive-going or negative-going edge of the clock pulse. The output may change several times in a single clock in the case of the level triggering circuit, whereas in the edge triggering course, the output will change only once in a unique clock.

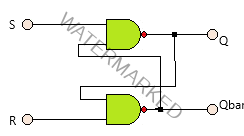
S-R Latch

The simplest type of flip-flop is called an S-R latch. Two cross-coupled NAND gates or two cross-coupled NOR gates are enough to design one, and the two inputs labelled S for set and R for reset. The two outputs are Q and Qbar. The S-R latch constructed using two cross-coupled NAND gates is below.

S	R	Qn+1	State
0	0	x	Forbidden
0	1	1	Set
1	0	0	Reset
1	1	Qn	Halt

The production of each gate is connected to one of the inputs of another gate. The S-R latch with two cross-coupled NAND operates with both data generally at one unless the state of the latch changes. The truth-table exhibits various stages of the latch. The last condition in the table is invalid when both the inputs are 0 at the same time. The state is called an invalid or forbidden state.

Design

module SR_latch(Q,Qbar,S,R);
input S,R;
output reg Q,Qbar;
nand n1 (Q,S,Qbar);
nand n2 (Qbar,R,Q);
endmodule

Test Bench

module SR_latch_Tb;
reg S;
reg R;
wire Q;
wire Qbar;
SR_latch uut (.S(S), .R(R), .Q(Q), .Qbar(Qbar));
initial
begin
$monitor(S,R,Q,Qbar);
$display(S,R,Q,Qbar);
$dumpfile("dump.vcd");
$dumpvars;
end
initial begin
S = 0;
R = 0;
#10 S = 0;
R = 1;
#10 S = 1;
R = 0;
end
endmodule

S-R Flip-flop

The Figure shows the clocked S-R flip-flop. The circuit is similar to S-R latch except for clock signal and two AND gates. The course responds to the positive edge of the clock pulse to the inputs S and R. Q and Qbar are outputs.

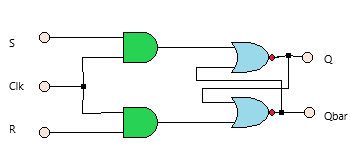
Following is the truth table.

Clock	S	R	Qn+1	State
1	0	0	Qn	Hold
1	0	1	0	Reset
1	1	0	1	Set
1	1	1	x	Invalid

Here, Qn represents the state of flip-flop before applying the inputs, and Qn+1 represents the state of flip-flop output after the application of input and clock. The characteristic equation is an algebraic expression for the binary information of the characteristic table. It specifies the value of the next state of a flip-flop in terms of its present state and present excitation.

The characteristic equation of S-R flip-flop is Qn+1=S+R’Qn. Disadvantages of the S-R flip-flop is the invalid states present when both the inputs S and R are made HIGH(logic 1). To avoid this difficulty, we use J-K flip-flop.

Design

module Main(input S,
input R,
input clk,
output Q,
output Qbar
);
reg M,N;
always @(posedge clk) begin
M <= ~(S & clk);
N <= ~(R & clk);
end
assign Q = ~(M & Qbar);
assign Qbar = ~(N & Q);
endmodule

Test Bench

module TestSR;
// Inputs
reg S;
reg R;
reg clk;
// Outputs
wire Q;
wire Qbar;
Main uut (
.S(S),
.R(R),
.clk(clk),
.Q(Q),
.Qbar(Qbar)
);
initial
$monitor(S,R,clk,Q,Qbar);
always #5 clk =~ clk;
initial begin
S = 0;
R = 0;
clk = 0;
#10 S = 0;
R = 1;
#10 S = 1;
R = 0;
end
endmodule

J-K Flip-flop

The J-K flip-flop is a refinement of the S-R flip-flop. In this circuit, the J-K class defines the indeterminate (invalid) state of the S-R type. The figure shows the logic diagram of J-K flip-flop with data input J and K ANDed with Q and Qbar respectively to obtain S and R inputs i.e.

S=JQ’

R=KQ

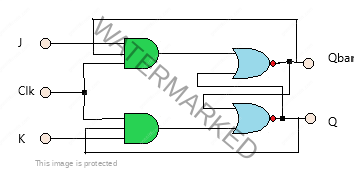
Clock	J	K	Qn+1	State
1	0	0	Qn	Hold
1	0	1	0	Reset
1	1	0	1	Set
1	1	1	Qn’	Toggle

Above is the truth table. The characteristic equation is Qn+1=JQn’ + K’Qn

Design

module jk_ff(q,clk,j,k);
input clk,j,k;
output reg q;
always @ (posedge clk)
begin
case({j,k})
2'b00: q<=q;
2'b01: q<=0;
2'b10: q<=1;
2'b11: q<=~q;
endcase
end
endmodule

Test Bench

module Testjk_ff;
reg clk,j,k;
wire q;
jk_ff dut (q,clk,j,k);
initial begin
$monitor(q,clk,j,k);
$dumpfile("dump.vcd");
$dumpvars;
end
always #5 clk =~ clk;
initial begin
j = 0;
k = 0;
clk = 0;
#10 
k = 1;
#10 
j = 1;
k = 0;
end
endmodule

D Flip-flop

From the truth table of S-R flip-flop, it is clear that the output of S-R flip-flop is in an unpredictable state. The unpredictable state is when the inputs are the same (i.e., when S=R=0, then Q= Halt and when S R=1, Q= invalid). Therefore in many practical applications, these input conditions seem unnecessary. Thus the modified S-R flip-flop which avoids such terms is known as D flip flop. The figure below shows a D flip-flop out of an S-R flip-flop.

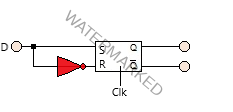
It is a flip-flop with delay equal to exactly one cycle of the clock. It is also called “data transmission flip-flop,” and “transparent latch.”

Clock	D	Qn+1
0	x	Qn
1	0	0
1	1	1

Qn=D is the characteristic equation of the flip-flop.

Design

module d_ff(q,clk,d);
input clk,d;
output reg q;
always @ (posedge clk)
begin
q<=d;
end
endmodule

Test Bench

module Testd_ff;
reg clk,d;
wire q;
d_ff dut (q,clk,d);
initial begin
$monitor(q,clk,d);
$dumpfile("dump.vcd");
$dumpvars;
end
always #5 clk =~ clk;
initial begin
d = 0;
clk = 0;
#10
d = 1;
#10
d = 0;
end
endmodule

T Flip-flop

T flip-flop is a single input version of J-K flip-flop and obtained by tying J and K input of the flip-flop. Moreover, the designation “T” comes from its ability to toggle or change its states. Below is the truth table of T flip-flop.

Clock	T	Qn+1
0	x	Qn
1	0	Qn
1	1	Qn’

The characteristic equation is Qn+1=TQn. Test Bench of the flip-flop will be same as others.

Design

module flipflop(q,qbar,clk,t);
output reg q;
output qbar;
input clk;
input t;
assign qbar = ~q;
always @(posedge clk)
begin
case(t)
1'b0: q <= q;
1'b1: q <= ~q;
endcase
end
endmodule

Race Around Condition

The difficulty of both the inputs to be ‘1’ in case of S-R of the invalid state is eliminated by a J-K flip-flop by using feedback connections from output to the input. However, the condition when(level triggered) J= K = 1 is not yet perfect.

Consider J= K = 1 and Qn = 0 and a clock (CLK) is applied. After a propagation delay time through two NAND gates, the output will toggle to Qn= 1. Since this is feedback to the inputs, the output will toggle back to Qn = 0 after another delay.

Thus, as long as the clock pulse is present, the output will toggle at every propagation delay, and at the end of the clock pulse, the value of Qn is uncertain. This situation will continue as long as the clock pulse width is longer than the propagation delay of each NAND gate. Such a case is referred to as the “race around the condition.”

Must read:

• Non-Arithmetic Combinational Circuits
• Designing Combinational Circuits through Verilog HDL
• Modeling of Combinational Logic Circuits

Conclusion

Sequential Circuits has a platter of real-life and textbook examples. Shift registers, counters, and state machines are the most common ones. They are useful in designing FPGA, PLD, CPLD, etc. In Designing Sequential Circuits through Verilog, I briefed each flip-flop and modelled it using Verilog. We will discuss Shift registers in the next section.