Designing Combinational Circuits through Verilog HDL

Combinational Circuits through Verilog

Designing Combinational Circuits through Verilog HDL: In the previous section, we discussed arithmetic combinational circuits. Certainly, there are ample combinational circuits in electronics with a broad spectrum of applications in Arithmetic Logical units, Processors, etc. So here we will look at all the remaining essential circuits along with their design codes.

Continuing the binary parallel adder, certainly, there are more models. One is Carry Look Ahead Adder.

Carry Look Ahead Adder

In the case of the parallel adders, one can calculate the speed by the time required for the carry to propagate or ripple through all of the stages of the adder. The look-ahead-carry adder speeds up the process by eliminating this ripple carry delay. Hence, it is better. The circuit below is an adder for a pair of bits.

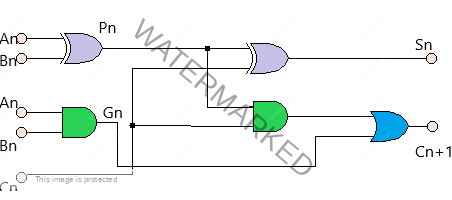
The above circuit is a full adder circuit. Firstly ‘P’ is the propagation term and ‘G’ is the generic term. Both terms are with respect to Carry.

Pn= An ⊕ Bn

G= An.Bn

Output sum ‘S’ and carry ‘C’ is as follows

S= Pn ⊕ Cn

Cn+1= Gn + Pn.Cn

For ‘n’ number of bits, we can cascade the above circuit ‘n’ times. It examines all the input bits simultaneously and generates the carry-in bits for all the stages simultaneously. For instance, a 4-bit adder Carry C3 does not have to wait for C2 to propagate. Propagation of all the Carries occurs at the same time. Therefore, that delay for output Carry reduced. However, the attainment of an increase in the speed of operation is at the expense of an additional highly complex circuit.

Below is the construction of a four-bit adder with a look ahead carry scheme.

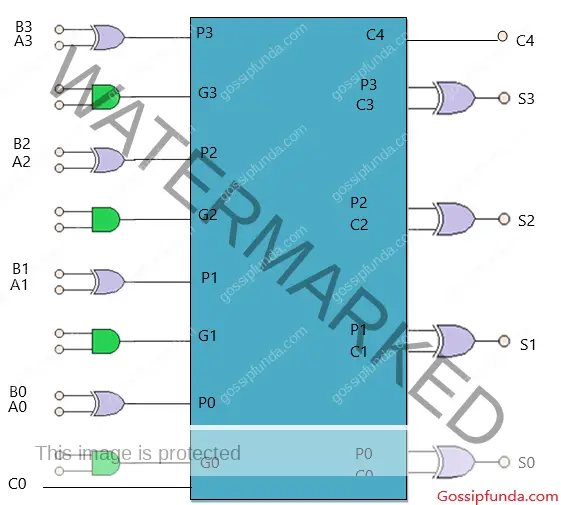
From the above diagram, equations Carry are

C0=input carry

C1=G0+P0.C0

C2=G1+P1.C1

On substituting equations, the final Carry C3 is

C3=P2.P1.P0.C0+P2.P1.G0+P2.G2+G2

Since the Boolean function for each output, carry is a sum of product form. The carry generator circuit is a 2-level implementation. The function is one level of AND gates followed by another level of an OR gate

Do not miss: Modeling of Universal and Special Gates on Verilog

Design

//Combinational Circuits through Verilog
module carry_look_ahead(a, b, cin, sum, carry);
output reg [3:0] sum;
output reg carry;
input cin;
input [3:0] a,b;
wire [3:0] p,g;
wire [4:0] c;
assign c[0] = cin;
assign sum[0] = a[0] ^ b[0] ^c[0];
assign sum[1] = a[1] ^ b[1] ^c[1];
assign sum[2] = a[2] ^ b[2] ^c[2];
assign sum[3] = a[3] ^ b[3] ^c[3];
assign c[1] = a[1] & b[1]|((a[1] ^ b[1]) & c[0]);
assign c[2] = ( ( a[1] & b[1] ) | ( ( a[1] ^ b[1] ) & ( ( a[0] & b[0] ) | ( ( a[0] ^ b[0] ) & c[0] ) ) ) );
assign c[3] = ( ( a[2] & b[2] ) | ( ( a[2] ^ b[2] ) & ( ( a[1] & b[1] ) | ( ( a[1] ^ b[1] ) & ( ( a[0] & b[0] ) | ( ( a[0] ^ b[0] ) & c[0] ) ) ) ) ) );
assign carry = c[3];
endmodule

Indeed, the code isn’t resembling any of the equations. Therefore, I simplified them to reduce delays. The generalized equation for Sum is P C, where P is AB. Consequently in the code, I wrote the final simplified equation.

Test Bench

module testbench;
reg [3:0] a,b;
reg cin;
wire [3:0] sum;
wire carry;
carry_look_ahead dut(a, b, cin, sum, carry);
initial
begin
a = 0; b= 0; cin = 0; #50; // Set inputs and add delay
a = 3; b = 2; cin = 1; #50; // Set inputs and add delay
a = 7; b = 10; cin = 0; #50; // Set inputs and add delay
b = 15; b = 15; cin = 1; #50; // Set inputs and add delay
end
initial
begin
$monitor( sum, carry, a, b, cin);
$dumpfile("dump.vcd");
$dumpvars;
end
endmodule

Difference between Serial and Parallel Adders

In the Combinational Circuits through Verilog, based on the manner of addition, a serial adder is another class of adders. As the name says, a serial adder adds two binary numbers in serial form. It is different from the binary parallel adder in the following ways.

1. A parallel adder uses registers with parallel loads but a serial adder uses shift registers. A separate article will be published shortly on the register. For now, consider serial register as the unit of digital electronics that stores and circulates the data within.

2. The numbers of full adder circuits in the parallel adder is equal to the number of bits in the binary number. On the other hand, a serial adder requires only one full adder and a carry flip flop.

3. Parallel adder, excluding registers, is a combinational circuit, whereas a Serial Adder is a sequential circuit.

Read more: Modeling Basic Gates through Verilog

BCD Adder

BCD or binary coded decimal is a 4-bit code where a binary equivalent represents a decimal number. It is a handy and convenient code. So it is used for input and output operations in electronics. For instance, 903 in binary is represented as 1001 0000 0011 in BCD code.

The BCD addition is a type of serial summation. For example, we add two 4-bit BCD code groups for every digit position using straight binary addition. So the SUM is in proper form for those positions where the sum is 9 (1001) or less, and no correction is needed. A correction of 0110 will be applied to the present total unless the total of two digits is greater than 1001 (decimal 9), and also the generated carry must be added to the following decimal position.

Logic

This conversion is essential from the hardware standpoint. In binary, the total number of representations for the 4-bit format is 2^4 or 16. Here, we have 10 valid code from 0 to 9. Hence only 6 invalid codes are left. Therefore, the conversion is done to subdue it.

Therefore unlike the binary parallel adder, the circuitry for a BCD addition must include the logic needed to detect whenever the sum is higher than 1001 (decimal 9).

For example, if the two BCD code groups A3 A2 A1 A0 and B3 B2 B1 B0 are applied to a 4-bit adder, the adder yields S4 S3 S2 S1 S0. In other words, S4 is C, the carry out of the MSB bits.

Two or more BCD adders can be connected in cascade when two or more digit decimal numbers are to be added. As a result, the carry-out of the first BCD adder is connected as the carry-in of the second BCD adder, the carry-out of the second BCD adder is connected as the carry-in of the third BCD adder and so on.

Design

module BCD(sum,cout,a,b);
output reg [3:0] sum;
output reg cout;
reg [4:0] temp;
input [3:0] a,b;
always @ (*)
begin
temp=a+b;
if(temp>9)
begin
temp=temp+6;
sum=temp[3:0];
cout=temp[4];
end
else
begin
sum=temp[3:0];
cout=0;
end
end
endmodule

Test Bench

module BCD_tb;
wire [3:0] sum;
wire cout;
reg [3:0] a,b;
BCD dut (sum,cout,a,b);
initial
begin
$monitor(sum,cout,a,b);
$display(sum,cout,a,b);
$dumpfile("dump.vcd");
$dumpvars;
end
initial
begin;
a=2;
b=9;
#10
a=2;
b=15;
#10
a=1;
b=6;
end
endmodule

Excess-3 Adder

The excess-3 adder is used for the addition of two excess-3 code groups. In this addition, if carry=, then add 0011 (decimal 3)to the sum of those two code groups. However, if carry=0, subtract 0011 (decimal 3). Considering that the audience is well aware of the concept of 2’s complement, we can add 1101 (decimal 13) to the sum of those two groups.

The design logic will remain the same as the BCD adder. Instead of add 0110 (decimal 6), 0011 is to be either added or subtracted in the if-else case.

Addition and subtraction are two basic functions. Therefore, digital electronics encapsulate subtractor circuit also.

Half Subtractor

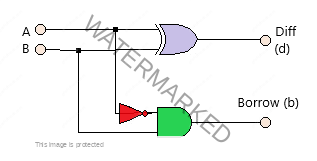
A half subtractor is a combinational circuit that subtracts one bit from the other and produces the Difference. That is to say, a half subtractor circuit with two input variables designated as A (minuend) and B (subtractend) and output variables as Difference ‘d’ and Borrow ‘b.’ Listed below is the circuit and truth table of half subtractor

A	B	Difference	Borrow
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

On analyzing the truth table, one can obtain the boolean expression for the same.

d= A’B+AB’ =A ⊕ B

b=A’.B

Alike any circuit existing in the digital electronics encyclopedia, the realization of Half subtractor is feasible through only NAND gate or only NOR gate.

Design

module halfsub(d ,bo, a, b);
output reg d, bo;
input a,b;
assign d= a ^ b;
assign bo= ~a & b;
endmodule

Test Bench

module halfsub_tb;
reg a,b;
wire d,bo;
halfsub dut(d,bo,a,b);
initial
begin
$monitor( a, b,d,bo);
$dumpfile("dump.vcd");
$dumpvars;
end
initial
begin
a=0;
b=0;
#100
a=0;
b=1;
#100
a=1;
b=0;
#100
a=1;
b=1;
end
endmodule

Full Subtractor

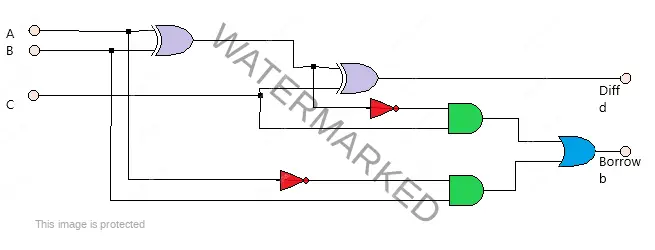
A full subtractor is an arithmetic circuit that performs a subtraction between two bits taking in the account that a lower significant stage may have borrowed a ‘1’. Thus a full subtractor has three inputs, namely A, B and C, and two outputs difference ‘d’ and borrow ‘b.’

The block diagram of a full subtractor is below along with the truth table.

A	B	C	Difference	Borrow
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

The logical expressions for Difference and Borrow are:

d= A’B’C+ A’BC’+ AB’C’+ ABC

d= A ⊕ B ⊕ C

b= A’C+ A’B+ BC

Implementation of a full subtractor circuit through NAND or NOR gates are convenient. Obeying the concept of design reusability, a full subtractor circuit is achievable with two half subtractor and an OR gate also.

Design

module fs(diff, borrow, a, b, c);
output reg diff, borrow;
input a, b, c;
assign diff= a ^ b ^ c;
assign borrow = (~a & c) + (~(a ^ b) & c);
endmodule

Test Bench

module fs_tb;
reg a, b, c;
wire difference, borrow;
fs dut(difference, borrow, a, b, c);
initial
begin
a=0; b=0; c=0;
#100 a=0; b=0; c=1;
#100 a=0; b=1; c=0;
#100 a=0; b=1; c=1;
#100 a=1; b=0; c=0;
#100 a=1; b=0; c=1;
#100 a=1; b=1; c=0;
#100 a=1; b=1; c=1;
end
initial
begin
$monitor( difference, borrow, a, b, c);
$dumpfile("dump.vcd");
$dumpvars;
end
endmodule

Conclusion

Till now, we discussed all Combinational Circuits through Verilog. So one should have to understand the importance of these circuits in electronics and its applications. Moreover, excelling in Verilog is necessary to gain expertise in VLSI. In upcoming articles, we will discuss the remaining combinational circuits.